« `html Le collagène marin gagne en popularité dans le monde du bien-être et de la beauté masculine, devenant un complément de choix pour ceux qui cherchent à améliorer l’apparence de leur peau. Dérivé de la pêche durable et souvent décrit comme le secret d’un visage plus jeune et d’une peau plus résistante, le collagène marin …

Choisir la Serviette de Plage Fouta: Qualité et Tendance au Rendez-vous
Quand le soleil commence à monter dans le ciel et que les vagues de l'océan vous appellent, il est temps de penser à la serviette de plage parfaite pour vos après-midi d'été. Parmi les nombreuses options disponibles, la serviette de plage fouta se distingue comme un choix de qualité, alliant tendance et fonctionnalité. Cet article …

Croisière sur le Nil : Un voyage intemporel au cœur de l’Égypte ancienne
Une croisière sur le Nil n'est pas qu'un simple voyage, c'est une expédition dans un monde où le temps semble s'être arrêté. Laissez-vous transporter dans un univers à la fois majestueux et mystérieux, où chaque méandre du fleuve vous raconte une histoire vieille de plusieurs millénaires. Embarquez pour une odyssée en plein cœur de l'Égypte …

Voyage au cœur du Serengeti : Immersion dans la vie sauvage africaine
Le Serengeti est l'un des joyaux de notre planète, une étendue sauvage qui représente l'essence même de l'Afrique. Ce parc national, situé en Tanzanie, s'étend sur plus de 15 000 kilomètres carrés et héberge une incroyable diversité de faune et de flore. Un voyage au cœur du Serengeti est une véritable immersion dans l'esprit de …

Améliorez votre tonus sexuel avec ces exercices physiques
Le tonus sexuel, une composante clé de la vie intime, n’est pas uniquement lié aux facteurs psychologiques ou à une alimentation spécifique. La forme physique générale joue également un rôle prépondérant dans la vigueur et la performance sexuelle. Dans cet article, nous allons explorer des exercices physiques ciblés qui peuvent non seulement améliorer votre tonus …

Plongée au cœur des séjours VTT : Aventure et déconnexion en pleine nature
Vous êtes à la recherche d’une échappatoire de la routine quotidienne, une quête de liberté, d’aventure et de connexion avec la nature? Alors imaginez-vous sur un VTT, traversant des sentiers sinueux, forêts majestueuses et paysages à couper le souffle. Les séjours VTT offrent tout cela et bien plus encore, promettant une expérience qui dépasse largement …

Après 40 ans, comment garder la ligne et rester en bonne santé
Atteindre la barre des quarante ans est souvent synonyme de changements physiologiques et métaboliques. Garder la ligne après cette période charnière nécessite d’adopter un mode de vie spécifique. Cela inclut une alimentation équilibrée, une activité physique régulière et une bonne gestion du stress pour rester en bonne santé. Les hommes après 40 ans sont confrontés …

Les vertus de la maca pour un tonus sexuel inégalé
« `html Introduction aux bienfaits de la maca sur la vitalité sexuelle La maca, plante ancestrale originaire du Pérou, est devenue célèbre pour ses multiples bienfaits sur la santé générale et la vitalité sexuelle en particulier. Surnommée le « ginseng péruvien », elle fait partie intégrante de la médecine traditionnelle andine depuis des millénaires et s’invite désormais dans …
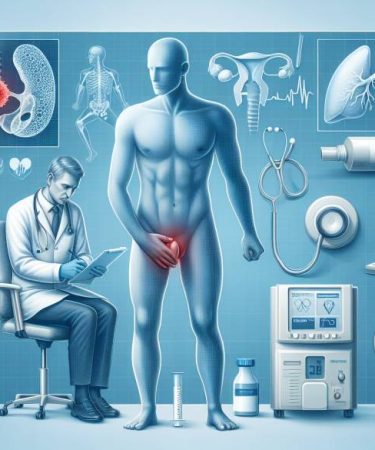
Comment identifier les signes d’un cancer des testicules
Comprendre le Cancer des Testicules Le cancer des testicules est une pathologie grave qui touche principalement la population masculine, et sa détection précoce est cruciale pour augmenter les chances de traitement efficace. Il s’agit d’un type de cancer qui se développe dans les testicules, responsables de la production des spermatozoïdes et des hormones sexuelles masculines. …

Créatine : utilisations et bienfaits pour l’homme en quête de performance
La créatine est un acide aminé présent naturellement dans le corps humain, et plus abondamment dans les muscles. Elle joue un rôle crucial dans la production d’énergie en régénérant l’ATP (Adénosine TriPhosphate), la principale source d’énergie cellulaire lors d’activités physiques intenses et de courte durée. S’ajoutant à cela, la créatine est également disponible sous diverses …